Metamerism - The Color Phenomenon Explained

Metamerism describes a pheonmenon where differently composited light leads to an identical color perception for the eyes of a human. Or looking at it the other way round: The same object under slightly different light suddenly has a different color.

You have perhaps experienced this when buying groceries: The deep red tomatoes on the vine you chose under the artificial store light turn out to be unripe fruits when looking at them at home. How can that be?

The problem of metamerism already bothered Isaac Newton in the 17th century. Luckily he wrote down his research in a letter to the British Royal Society in 1672. As the letter survived the centuries, we can still read about his endeavors.

As Newton wanted to create better telescopes, he began grinding his own lenses in 1666. In the course of his preparations, Newton also acquired a glass prism for experimenting. He darkened his workshop and only let the sun shine in through a small, round hole in the window cover. Into the ray he placed the prism and enjoyed the play of colors that emerged. Then a peculiar fact catched his eye: The light spot that emerged behind the prism wasn't round, like the hole it came through, and like it would look like without a prism in the way, but rather narrow and almost rectangular. The iluminated spot was about five times wider than it was high. This observation awakend his inquiring mind. Why did the spot have that particular form, and why the 5:1 ratio? Newton put forward a variety of theses: The reason could be the thickness of the glass the prism was made off, or the dimensions of the hole in the darkened window, or the position of the prism in the light ray. But none of these factors changed the appearance of the light spot emerging behind the prism.

Newtons next suspicion targeted irregularities in the glass itself. He bought a second, otherwise identical prism and conceived a new experimental setup: The refracted light behind the first prism should be brought back on track by placing the second prism into the light ray. The thesis he wanted to examine: The light that was not scattered by irregularities in the glass would continue on its original path, as if the two prisms would have not been placed there in the first place. This way the irregularities would be made more prominent, supporting Newtons theory.

The result: While the light coming through the window could indeed be returned to its original form by the second prism, no traces of scattered rays from faults in the prism glass could be observed.

Luckily, Newton didn't surrender yet. After several not very fruitful attempts to solve the case by mathematical means (He meticulously measured all distances, spot diameters, angles of refraction etc. and examined them for connections), he had a new hunch.

While watching tennis games, Newton had observered on several occasions that the ball, after being hit by a racket made from solid wood, flew along a curved line. According to Newton the ball simultaneously performs an angular motion along its own axis and a straight motion along the tennis parcour. At the point where angular motion and straight motion come together, the ball has to overcome more air resistance than at the opposite site - which would lead to a change of direction.

Perhaps, thought Newton, this is also the case with light rays when they emerge from the prism? Perhaps they act like round bodies performing a radial motion around themselves? Then there would be higher resistance on one side, leading to a deviation to the opposite side of the line described by the rays. But then the light would also move along a curved line - and the observed path was perfectly straight. So this approach also turned out to be a dead-end.

An additional experimental design finally turned out to be fruitful. Newton continued to use the original spot in the window blind. Into the light he placed a prism. Behind the prism he positioned a wooden board that, too, had a small hole. Three meters behind this board came a second, identical board, and behind that board Newton placed the second prism. After emerging from the second prism, the light illuminated a spot on the rear wall of his workshop.

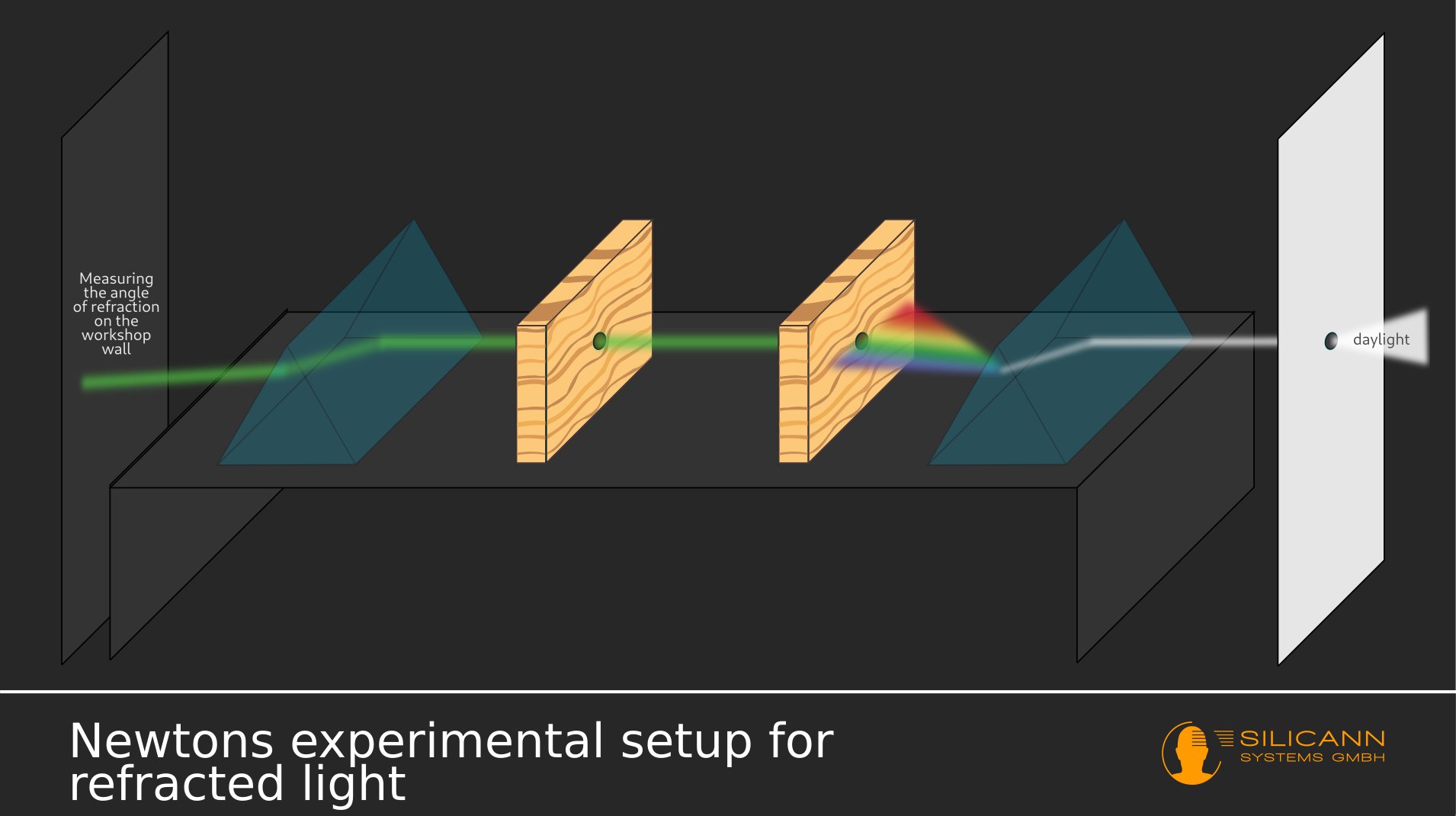
Newton now slightly moved the first prism in the array to and fro so that only a small part of the fanned out rainbow made it through the hole in the second board. This way he could systematically observe in which angle of refraction the specific part of the rainbow landed on the wall. The result: The refraction was higher on one end of the rainbow than on the other.

Newton concluded that the curious 5:1 relation of the fanned out light spot resulted from the different angles of refraction of the light rays. The different angles made the light spots appear at different locations of the wall.

Further experiments made clear that the individual light rays of a particular color always have the same angle of refraction. Additionally, both properties, color and angle of refraction, each predicted the other: From the angle of refraction one could defer the color of the light and vice versa. And the color red led to the smallest angle, while deep violet always produced the largest.

Newton observed another detail: The rays seemed to preserve these properties even when he mixed them differently: In one experiment Newton split composited light into distinct colors and merged them together afterwards. Newtons astute conclusion: Apparently not the light rays themselves change, but only our perception of them.

That taken by itself already was a major insight, because up to that moment colorfulness had been assumed to be a property of the objects themselves, and not one of the light illuminating them.

When splitting the visible sunlight using a prism, Newton observed seven distinct colors, which he called primary colors: red, yellow, blue, violet, orange and indigo, and of course arbitrary blends of those. Today these distinct colors are called spectral colors or colloquially rainbow colors.

And then Newton had the groundbreaking insight thanks to which he could expain metamerism, among other phenomena: These primary colors could be mixed together! A combination of yellow and blue rays resulted in a green ray, red and yellow together created an orange light ray etc. Newton even recognized the principle behind these observations: In the rainbow spectrum the two source rays had to have about the same distance from the primary color to create the same color perception when being mixed together.

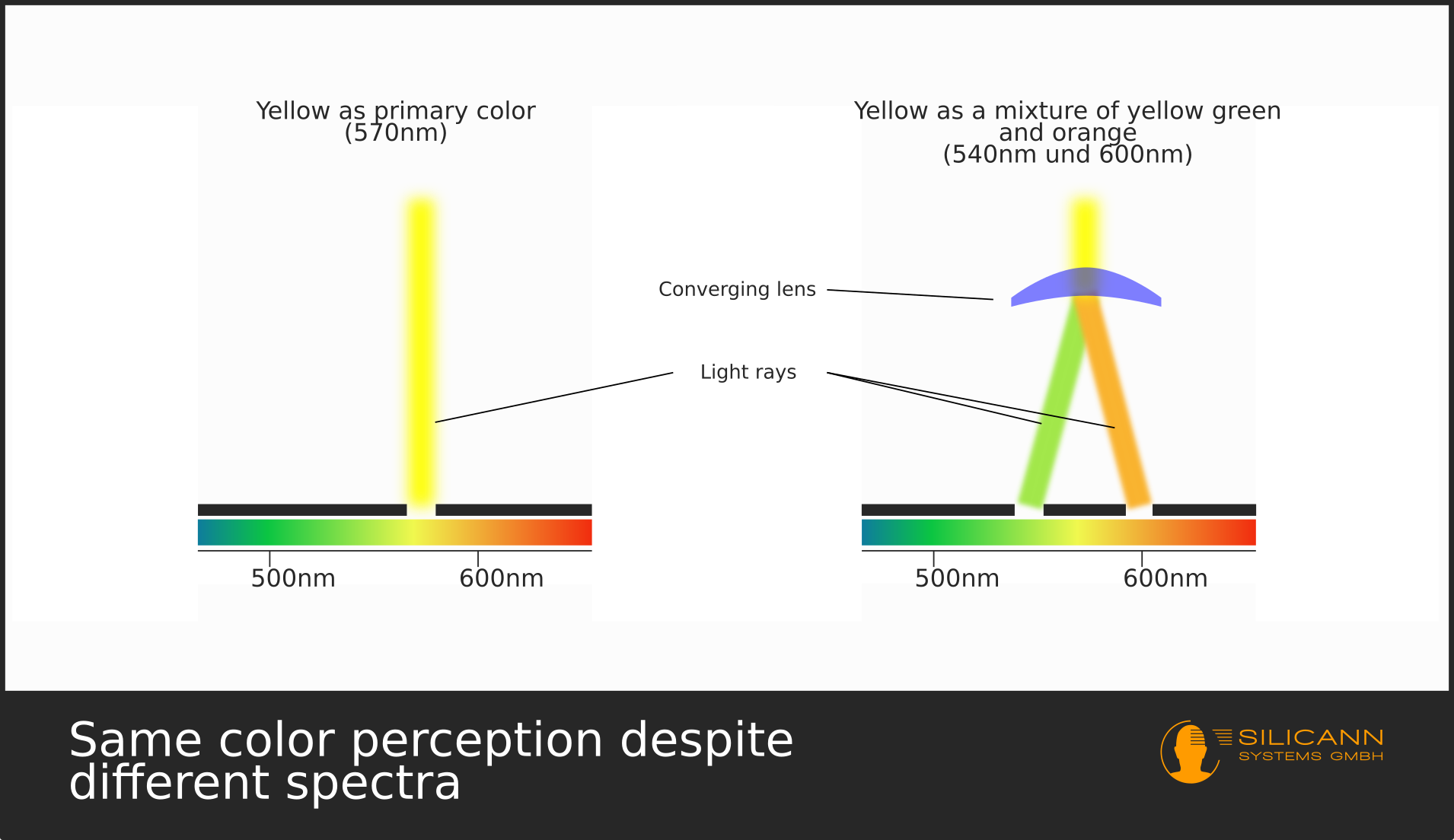
With these observations Newton left us the first written evidence for metamerism - albeit he did not yet call the phenomenon as such.

On a related note, Newton also warned us of a constraint when trying to mix together differently colored light: This will only work if both source rays are not too distant from each other. Mixing orange and indigo won't result in green.

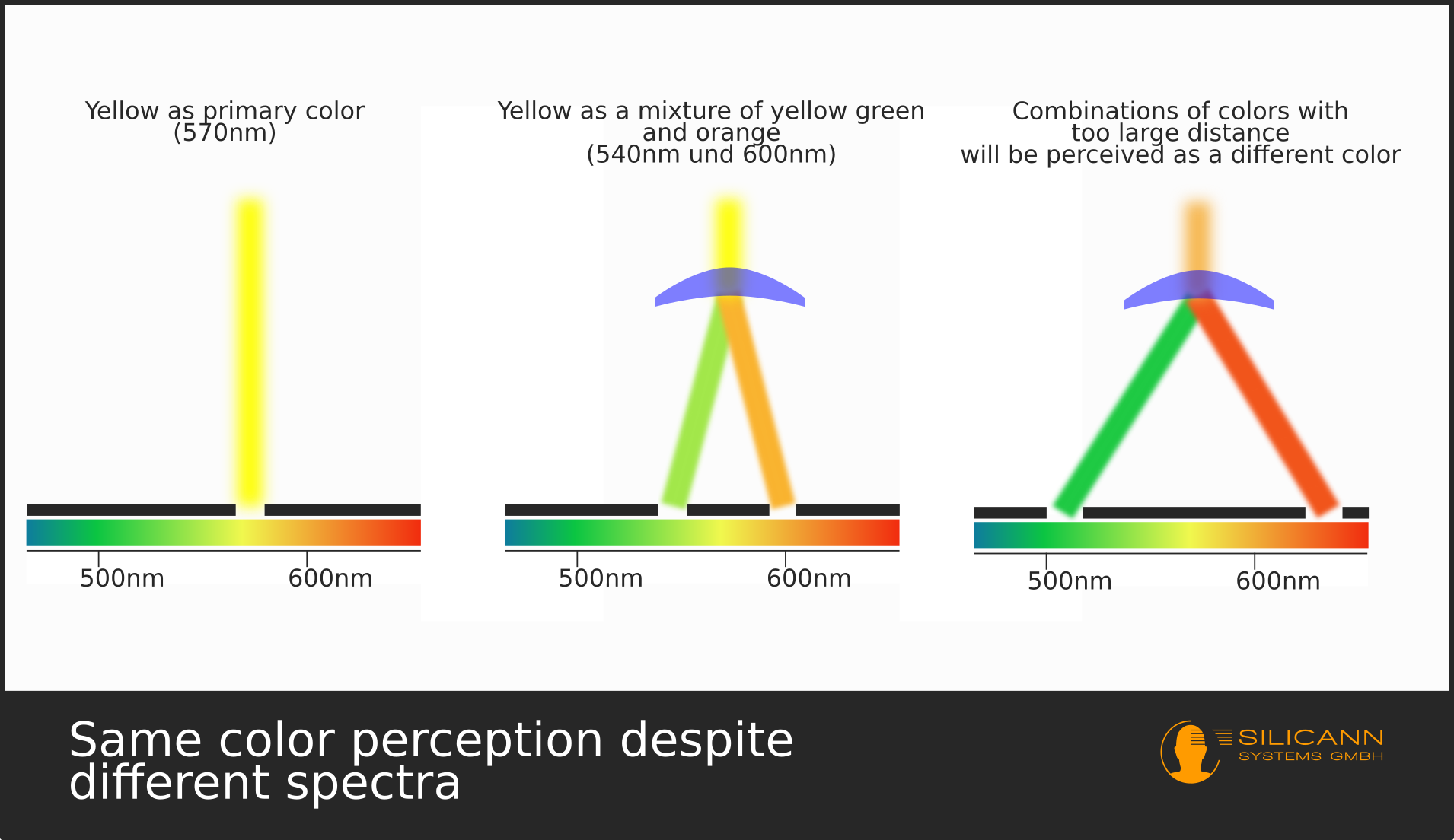
Why is that the case? Without knowing it, Newton got on to a limitation of human color perception. The human eye only sports three types of receptors. Each of these receptors, called cones, are only sensitive to a particular part of the visible spectrum. According to their particular sensitivity for specific wavelengths, they are named S cone (for shortwave, the blue end of the spectrum), M cone (for medium, the green range) and L cone (for longwave, the red range).

Now we actually can see more than these three colors in everyday life. How does this work? Our brain uses the signals of all three cones in a clever way: First, we directly get the cone signals and perceive them as particular colors. But the signals also get interconnected with each other, the results of which we also perceive as particular colors. For example, we cannot directly sense yellow, meaning a wavelength of about 570nm, simply because we lack cones with sensitivity in that spectral range.

And yet we can cleary see the yellow of e.g. a sunflower. This happens if the interconnected signals of the L cone and the M cone reach a certain ratio.

This explains the observation Newton has written about. The light ray is perceived as yellow if the subtraction of the signals of both cones has a specific result. But of course quite a few subtractions can result in the same value: Two minus two equals zero, but five minus five also equals zero. This explains Newtons findings: As long as M cone signal and L cone signal subtracted from each other result in the same value, we will perceive these light rays as having identical colors.

But at a certain point we will reach the edge of the sensitivity curve of one of the cones. The actual light may shine with identical intensity (only in a different spectral range), but our cone responsible for this range won't have the sensitivity, and thus the signal it emits will differ. Consequently the difference of the two cones' signals will result in a different value - and we will perceive the light as having a different color.

This also explains how metamerism happens: Two objects, appearing to be of identical yellow color when looked at under e.g. daylight, could actually reflect quite different spectral patterns. While one of the objects reflects a narrow band of around 570nm (yellow), the second object perhaps reflects both at 530nm (yellow green) and 610nm (orange). The average of these two spikes in the spectrum also results in 570nm. The combined signal resulting from the interconnection of the M cone and L cone produces the same result as for the first object. To our human eyes, both objects will have the same color.

That illusion will break in the moment the environmental illumination changes. Perhaps you have an LED desk lamp with a bit weaker emission in the green spectrum. Looked at under this lamp instead of sunlight, the second object will apparently change its color: If less yellow green reaches the object, it can also reflect less of it into our eyes - and in our perception the color of the second object will shift into the orange range. That is metamerism.

Sometimes metamerism is an unwanted effect, particularly in industrial production. An example would be a bicycle with a painted metal frame and a saddle made from synthetic material in a fitting color. The frame paint is expected to fit the color of the saddle - and not only under the artifical light of the sales room, but also under sunlight. The human color perception alone is not enough to ensure that. To select a fitting paint for the frame, we have to know more about the composition of the light that gets reflected by the paint. This is what spectrometers like Spektralwerk are used for. Unlike with color sensors, which only report the color impression as a whole, a spectrometer reports back the detailed composition of the light - not unlike Newtons final experimental design did on the workshop wall. The light gets refracted on a grid or a small slit, fanning out the rays. This means the radiation intensity can be measured for each particular wavelength. This way the spectral information itself can be processed. Thus yellow as a primary color or as a mixed color can clearly be seperated with the help of a spectrometer. Based on the spectral information that gets revealed after measuring the paint on the bicycle frame, one can evaluate the risk of metamerism without having to manually check the paint under different light sources.

Metamerism also gets exploited by the grocery stores illuminating the tomatoes. Even unripe fruits will reflect a certain amount of radiation in the red range of the visible spectrum. But they will also reflect green light, which would shift our impression of the aggregate color into the green. Grocery stores employ the metamerism effect to hide the green parts by installing light sources that don't replicate the neutral white of our sun, but instead emit most light in the yellow-red range. That way more red reaches the vegetables, which now can reflect more red and thus delude us into believing the tomatoes are riper than they really are.

Pro tip: The normal store illumination usually is more neutral white. Just grab the tomatoes and look at them outside of the deceptive light cone directly above the vegetables. This way you can outwit metamerism and get vegetables that actually are ripe.

By the way, If you directly want to read Isaac Newtons Letter, which still is suprisingly readable, here you can get it as a PDF file.